富山大学 研究者インタビュー#43
2025年11月10日

松本 知己 先生
富山大学 社会科学系 特命助教
松本先生は、ベイズ統計学を基盤に、より柔軟なモデルを社会実装するための理論研究と、
実社会の課題を題材とした実証研究に取り組んでいます。
幼いころから社会の仕組みに興味を持ち、社会工学を専攻した松本先生は、データサイエンティストとして社会で経験を積んだのちに、富山大学経済学部で統計学を中心とした独自の研究を始めました。
「統計学にのめり込んだのは、大学のころに『データ解析』という授業を受けたことがきっかけです。自動車の特性がずらっと並んだデータとその販売価格のデータを題材に、自動車特性から販売価格を説明するための回帰モデルを作るという授業でした。それまでに習った統計学の知識を使って実際のデータを分析してみると統計学が魔法のように感じました。統計学の中でも、直感的にわかりやすいベイズ統計学に関連する研究を学生時代から現在まで続けています。」
ベイズ統計学は、18世紀中頃にトーマス・ベイズによって発表されたベイズの定理に基礎を持ち、意外にも古い歴史がありますが、その性質からコンピュータのない時代には実用性が乏しいものでした。20世紀終わりのコンピュータの台頭により再評価され、年々論文数も増加しているホットな学問分野となっています。
そもそも統計学とは、不確実な世界を理解し、よりよい判断を導くための学問です。目的は『この範囲にある可能性が高い』『このくらいのばらつきがある』といった不確実性を含んだ知識を得ることで、通常『確率分布』という形で表現されます。
学校で学ぶ統計学は『頻度主義統計学』と呼ばれ、パラメータ(母集団の特性を表す数値)には『真の値』が存在すると考えます。例えば、日本人男性の平均身長は170cmだとすれば、観測されたデータ(168cm、175cmなど)はその周辺にばらついていると考えます。頻度主義における統計分析は、その真の値をデータから推定する作業となります。
一方、『ベイズ統計学』では、パラメータに対する私たちの不確実性を確率分布で表します。パラメータについての事前の知識(事前分布)にデータを加え、ベイズの定理を用いて知識を更新することで、より確からしい知識(事後分布)に更新していくのが特徴です。これにより、複雑な現象も直感的にモデル化できるのです。
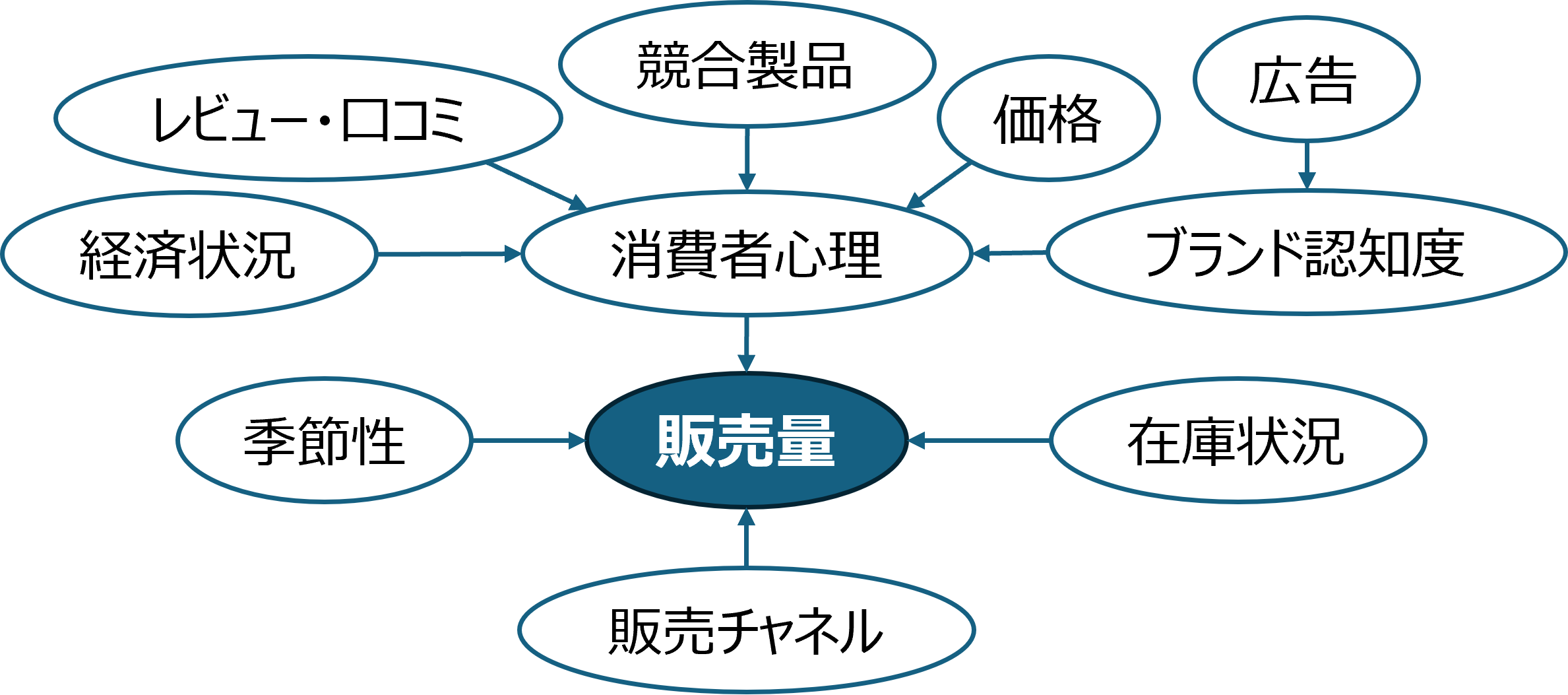
図1 商品の販売に関わる要因ネットワークの一例(筆者作成)
ベイズ統計学ではこのような複雑な関連性をモデルで表すことができ、それぞれの要因には固定値ではなく、確率分布を条件として与えることができる。
「例えばある商品の販売を考えると、価格、消費者の心理、競合製品の影響、個人の経済状況など、不確実な要因が多く絡み合ってきます。こうした要因同士の関係性は、図で描いて矢印で表すことで視覚的に表現できます(図1)。このような複雑な構造を統計学で分析しようとすると、頻度主義統計学では各要因の効果を固定された値として扱うため、確率分布を与えて不確実性を直接表現することは基本的に行いません。理論的には構造方程式モデル(SEM)などの手法を用いることで推定は可能ですが、計算が複雑になりやすく、線形や正規分布といった仮定に依存することが多いように感じます。一方でベイズ統計学では、各要因や潜在的な心理的要素にも確率分布を通じて不確実性をもたせることができます。その結果、複雑な階層構造や非線形な関係も自然に扱うことができ、自分の知恵を絞れば、その現象を説明する多様なモデルを柔軟に考えられるという点がベイズ統計学の大きな魅力だと思います。もっとも、ベイズにしたからといって計算の難しさが完全に解決するわけではありません。ただ、マルコフ連鎖モンテカルロ(MCMC)法と呼ばれる推定のフレームワークが整っていることは、ベイズ統計学の大きな強みだと思います。」
ベイズの定理で導かれる事後分布は、式として得られても複雑な形になることが多いため、平均や分散といった性質を理解するために、事後分布に従うサンプルを取り出すことができると便利です。しかし、複雑な分布から直接サンプルを得るのは簡単ではありません。
そこで使われる定番の方法がマルコフ連鎖モンテカルロ法(MCMC法)です。シミュレーションでサンプルを生成し、事後分布を近似する方法ですが、ここにも課題があります。MCMC法では1つ前のサンプルをもとに次のサンプルを生成するという逐次的なアルゴリズムであるため、モデルの複雑さやデータの容量・次元が増すほど計算に時間がかかるのです。
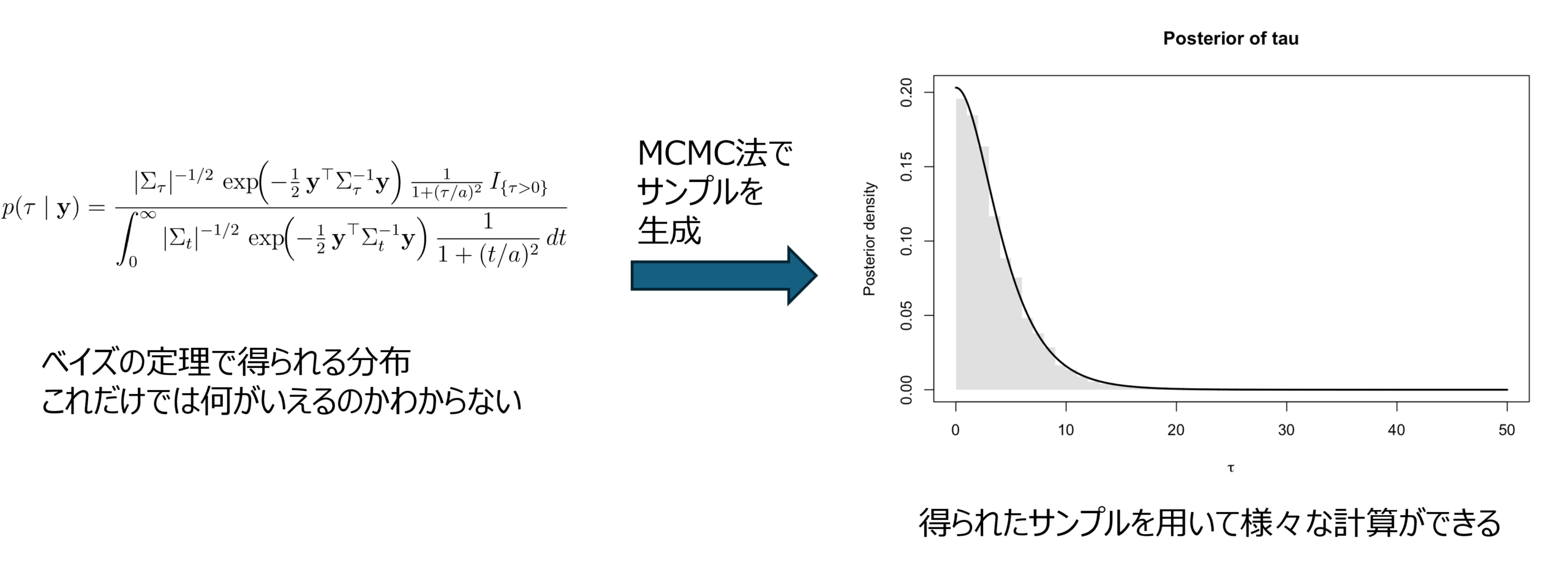
図2 MCMC法のイメージ図(松本先生ご提供、筆者にて加工)
「MCMC法にかかる計算時間を短縮するために、取り組んできたのが、MCMC法の並列化です。データを分けて、それぞれでMCMCを実行し、最後に結果をまとめるという方法です。『まとめる』方法について課題があるのですが、これまでの研究から一方で、複数の分析結果を結合することで、全体としての理解が深まっていくというやり方は、まさにベイズの考え方である『知識の更新』という本質に関わっていると感じています。今後は、MCMCの並列化に取り組みながら、結果の統合をベイズ更新として位置づける発想も取り入れ、両方向から柔軟で実用的な方法を探っていきたいと考えています。」
松本先生は理論研究だけでなく、実社会の課題を題材とした実証研究も行っています。現在取り組んでいる研究の一つに、デジタルニュース配信プラットフォームと記事提供元(出版社)間で交わされる記事掲載料適正性を分析・評価するものがあります。公正取引委員会のアンケート結果によるとデジタルニュース記事の掲載許諾料に関して出版社が不利益を被っている可能性が示唆されており、その実態をデータで明らかにすることを目的としています。
「アンケートでは回答がさまざまなバイアスの影響を受けうるため、実態や問題の程度を厳密に捉えるのは容易ではありません。この研究では、二者間の交渉を数理モデルで表し、実際のデータとつき合わせながら、モデル内のパラメータを推定・解釈することで、より客観的な示唆を導き出したいと考えています。」
今後も、社会や身の周りで起きていることを理解するため、統計学を活用して、経済・経営・マーケティングなど幅広いテーマの実証研究を行っていきたいとお話していただきました。
現在は一人一台パソコンを持ち、今後は皆が当たり前にデータ分析を行う未来が考えられます。データサイエンティストとしての経験がある松本先生は、現在のデータ分析の課題として、間違いに気づきにくいという点に着目されています。
「データ分析には答えがないので、『本当にこの結果を報告していいのか』と不安になることがあると思うんです。今後の夢として、データ分析の専門家でなくても、皆が正しく分析ができる未来に貢献できたら、と考えています。可能な限り、分析の方法論を整理して、こういうふうに分析して結果を解釈すれば、ある程度信頼できる結果として色々使えるよというフレームワークの開発に繋がる研究ができればと考えています。」
ベイズ統計学は、ビル・ゲイツ氏が『21世紀のマイクロソフトの戦略』と位置づけたことで注目を集めました。松本先生の理論と実践の両輪を回す研究は、今後、より広範囲なビジネス領域での応用可能性を広げるものだと思います。
学術指導・共同研究等のご相談はOneStop窓口からお願いします。
(文責:学術研究・産学連携本部 コーディネーター 浮田)
松本先生ホームページ https://sites.google.com/view/t-matsumoto/
富山大学研究者プロファイルpure https://u-toyama.elsevierpure.com/ja/persons/tomoki-matsumoto
Researchmap https://researchmap.jp/t-matsumoto514